引用:
作者: JOHN
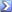
假設:只抽一次
中三球或四球或五球的機率
活跳跳的羅輯關念是正確的
因為排除了,中五球、中四球、中三球的機率再減除一
就為假設狀況的機率
答案為0.2808
也就是依機率來看,每抽100次,會有28次,抽中如上假設狀況
猜董所說,相加的狀況,應是,抽二次,抽三次
多數獨立事件,總機率就應該是各分別機率的加總
只抽一次,僅能以相關事件視之,機率應無相加的可能
以猜董所列公式,解答為176/252即0.6984
抽一次中三球的機率為0.1984
而0.6984顯然比,抽三次,中三球的機率高出甚多
抽一次,就能比抽三次最容易中的機率還高
似有商確的餘地....
|
機率用加法原理是因為他們乃互斥的樣本空間
比如台北到高雄,公車有三條路線,火車有兩條,那麼有幾種走法,有五種,3+2,因為走了這條另一條就不用了,所以是彼此互斥,同樣的,當你抽一次,有可能中五球,當然也可能四球,或三球,彼此互斥,所以機率是越大,要加,本題是中三個以上的數字,那我也不該再用1減,應該是1/252 + 25/252 + 50/252=76/252
乘法原理則是用在相關事件,比如台北到台中有公路三條,台中到高雄有兩條,那台北到高雄共有多少走法?共六條,2*3=6,所以,機率用乘的是指相關事件,例如玩三次,第一中五個數字,第二次四個,第三次三個,所以是1/252 * 25/252 * 50/252