[cwvdavid]

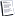
第三題，
用公式來導...

A(0: m-1, 0:n-1)
已知 s1 = 0, s2 = 0

接著已知 A(3,2) 在1110, A(2,3) 在1115
且元素佔一個空間，意即 d = 1


帶入公式(我繼續用第一題的公式)
A(i,j) = A(0,0) + ((i - s1) * n * d) + (( j - s2 ) * d)
A(i,j) = A(0,0) + ((i - 0) * n * 1) + (( j - 0 ) * 1)
A(i,j) = A(0,0) + (i * n) + j
(以上是簡化後的結果)

A(3,2) = A(0,0) + (3 * n) + 2 = 1110
→ A(0,0) + (3 * n) + 2 = 1110
→ A(0,0) + (3 * n) = 1108
→ A(0,0) = 1108 - (3 * n)

A(2,3) = A(0,0) + (3 * n) + 2 = 1115
→ A(0,0) + (2 * n) + 3 = 1115
→ A(0,0) + (2 * n) = 1112
→ A(0,0) = 1112 - (2 * n)

再將2者 拿來比較
1108 - (3 * n) = 1112 - (2 * n)
1108 - n = 1112

可以得到 n = -4 ...(行數是-4.........)

...到這裡出了問題了
因此，這個陣列【並不是 以列為主】

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
算我倒楣!!(對你來說是幸運，可以看到用錯公式時的情形)
．．．
所以，再重算一次，改用另一個公式，以行為主

A(i,j) = A(0,0) + ((j - s2) * m * d) + (( i - s1 ) * d)
A(i,j) = A(0,0) + ((j - 0) * m * 1) + (( i - 0 ) * 1)
A(i,j) = A(0,0) + (j * m) + i
(以上是簡化後的結果)

A(3,2) = A(0,0) + (2 * m) + 3 = 1110
→ A(0,0) + (2 * m) + 3 = 1110
→ A(0,0) + (2 * m) = 1107
→ A(0,0) = 1107 - (2 * m)

A(2,3) = A(0,0) + (3 * m) + 2 = 1115
→ A(0,0) + (3 * m) + 2 = 1115
→ A(0,0) + (3 * m) = 1113
→ A(0,0) = 1113 - (3 * m)

1107 - (2 * m) = 1113 - (3 * m)
1107 = 1113 - m
m = 6 因此...陣列大小A(0 : m-1, 0 : n-1)

就是 A(0:5, 0: n-1)
由於題目只問到 A(1:4)，所以 n 大於 4... n=5,6,7... n=無限大 也可以
(在這裡... n 用不到了...)

接下來，算一下A(0,0)的位置...
A(3,2) = A(0,0) + (2 * m) + 3 = 1110
A(3,2) = A(0,0) + (2 * 6) + 3 = 1110
A(3,2) = A(0,0) + 15 = 1110
A(0,0) = 1110 - 15 = 1095


A(2,3) = A(0,0) + (3 * m) + 2 = 1115
A(2,3) = A(0,0) + (3 * 6) + 2 = 1115
A(2,3) = A(0,0) + 20 = 1115
A(0,0) = 1115 - 20 = 1095

經由上面２個座標比對，確定A(0,0)是1095

最後，再計算 A(1,4)的值
A(1,4) = A(0,0) + (j * m) + i
A(1,4) = 1095 + (4 * 6) + 1
A(1,4) = 1095 + 25
A(1,4) = 1120 !!!!


(明明應該是你自己要看的公式，你自己都掃瞄了，也貼上來了
結果變成是我得幫你寫出來．．．．．．．．．．．唉．．．．．．．．．．)

上面這一題的陷阱就是　【以行為主】 v.s 【以列為主】
而要弄的懂，最好是把第二題，也算一算．．．．

也就是說：最好是從第一題開始算，算完之後再算第二題，再算第三題．．．
當你全部的習題都會算的時候，你這一章才能算是　真的了解了．．．．

而你如果中間的題目就這麼跳過去，不看了，
那你後面的章節只會更痛苦．．．．．

（很多資工科系，資管科系的學生　　之所以會裁在程式設計的課程，
就是因為一開始沒弄懂，後面更痛苦，最後放棄....）