財經 - 貨幣的時間價值

[猜謎人]

　　這篇文章如果是學過會計的人看了，可能就覺得不值得一哂，因為，這篇都是省略過的。但在這裡是想要簡單說明這些觀念，所以，也就把它拿來說一下！希望能有助於了解複利和年金的概念。
一、 複利終值
　　什麼是複利終值？在此我們一律用口語說明，不用難懂的專有名詞。舉個例子來說，如果存入一筆錢，那麼，假設十年後會變成多少錢？當我們存入之後，每半年會算一次利息，但是，下一次計算利息時，之前的利息會併入本金來算這次的利息，於是，錢又滾錢，到最後會變成多少錢，這個數字我們稱之複利終值！
　　以下圖來說明：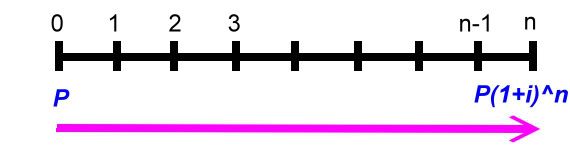



　　如果在年初存入本金P，經過一段時間，其複利終值就是P(1+I)^n，其證明如下：



　　第一期的利息是本金P乘上利率i，也就是P*i！
　　第一期的本利和S1就是本金P加上利息I1，也就是P+I1，其中I1又是P*i，所以，S1=P+P*i，我們提出公因數P，於是，S1=(1+I)P。
　　第二期的本金已經不是P了，而是S1，因為，第一期的利息滾入本金來算第二期的利息，同樣的，第二期利息就是S1*i。
　　第二期的本利和就是S1+S1*i，也就是P(1+i)+P(1+i)i，同樣提出P(1+i)，所以式子變成(1+i)P(1+i)=P(1+i)^2。
　　後面就都一樣了，結論就是n年後，本利和就是P(1+i)^n，這個就是複利終值的公式。
　　我們舉個實例，假設小護士要存自己的結婚基金，於是存了＄200,000到銀行，當時年利率是4%，小護士預計五年後可以使用，以台灣每年一月和七月計息，也就是一年複利兩次，五年複利10次，利率是4%/2=2%複利終值如下：
　　　　　S=200,000(1+2%)^10=243,798.88
　　多了43,798.88元！
　　這裡要說明一下，一般我們都把本金當作一元，如此，我們只要有(1+i)^n這個數值，那麼，只要知道本金，去乘以(1+i)^n就可得到結果，在財務上，我們可以稱(1+i)^n叫做複利終值，過去都是查表得知，現在電腦這麼方便，我們可以直接算，或用軟體計算。
二、 複利現值
　　現在我們反過來，把複利終值的觀念倒轉一下，如果我們經過十期之後想要領到＄200,000，那麼，我們現在要存在銀行多少錢？這時候，我們的終值就是＄200,000，我們現在要求的是本金P，以下圖來看：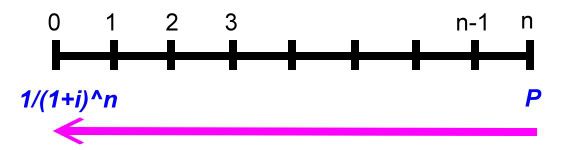



以計算式子來說明：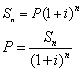



　　已經知道終值Sn，(1+i)^n也已知，現在要求P，我們只要移項，就可得到複利現值的公式！
同樣的，我們在此把Sn當作一元，也就是未來要得到一元，現在要存多少錢？如果有了1/(1+I)^n，那麼只要知道未來的金額，只要相乘即可！
　　舉實例來看，卡拉五年後想要買台汽車，假設想要五年後有＄200,000，那現在要存多少錢？同樣的，年息4%，一年複利兩次，複利10期，利率是4%/2=2%
P=200000/(1+2%)^n=164069.65997
　　卡拉，快去存吧！
三、 年金終值
　　現在，我們要來點難的了，其實，說難也不難，就是要花一點心思，我們要說的是年金終值！什麼叫做年金？所謂年金就是每一期末交付一定的金額來作複利，我們之前複利終值是指期初存一筆金額，一直不動看最後能複利多少？現在是每年年底都存一定金額作複利，以下圖來看：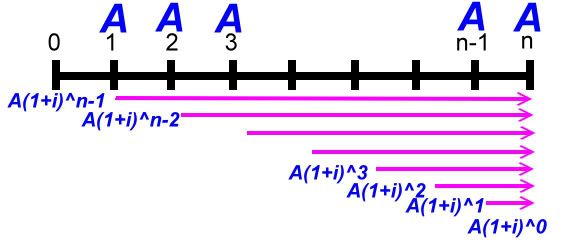



　　第一期期末存一定金額A存到最後我們可得終值A(1+i)^(n-1)，第二期期末又存一定金額A存到最後我們可得終值A(1+i)^(n-2)，每期都存！最後我們給加起來就是我們最後可得到的年金終值！你會說那我們不能期初來存？可以的，這種我們稱他期初年金，又或者問為什麼要存一定金額，金額不同不行嗎？當然可以！這種我們叫做變額年金，不管如何，這些都是特殊不同的，在此我們只討論期末交付一定金額，這種我們稱普通年金。
現在我們要把這些加起來推算公式，證明如下：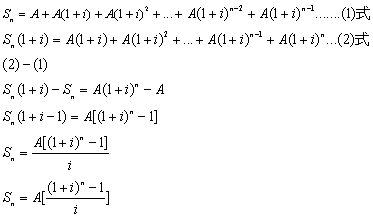



　　第一式就是我們把每一期末交付的金額A，複利到最後的總合，我們把第一式的兩邊同乘上(1+i)變成第二式，然後，把第二式減去第一式得出
　　Sn(1+i)-Sn=A(1+i)^n－A
　　把Sn和A提出來再移項
　　公式完成！一樣的我們若把交付金額當作一元，[(1+i)^n－1]/i就是年金終值公式！
　　舉實例，小q想要一發久久久，所以，他打算每半年存＄100,000，存十年後，他有多少錢？
一樣，一年複利兩次，十年共二十期，年息4﹪，利率4﹪/2=2﹪：
Sn=＄100,000{[(1+0.02)^20－1]/0.02}=＄2,429736.98
　　小q你發了！
四、 年金現值
　　這個是年金終值相反的觀念，我們直接舉個實例來看，如果我們想在未來的十年，每半年可以領＄100,000，十年剛好領完，那我們現在要存多少錢到銀行？也就是說，十年內每半年領的＄100,000，現在是值多少？以下圖來表達：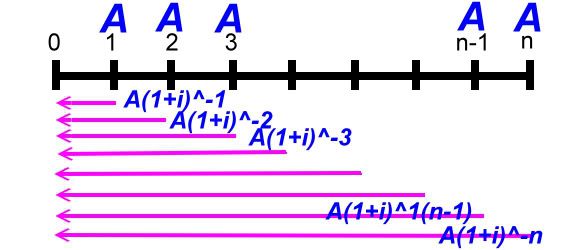



第一期末的年金A折算到現在，第二期的A也折算到現在，每一期都折算到現在，再把他們全部加起來！這個就是年金現值，現在我們來證明其公式，如下面的證明內容：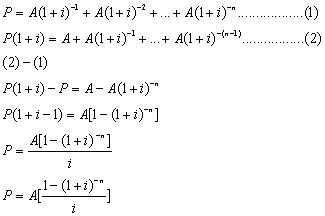



　　第一式的P就是年金現值，把每一期的支付A都折現到現在，我們把第一式的兩邊乘上（1+i），這就成了第二式。
一樣，把第二式減去第一式，再左邊提出P，右邊提出A，移項即可得出P，同樣，我們假設年金A是一元，把右式整理一下，那麼[1-(1+i)^-n]/I就是年金現值的公式！
　　舉個應用例子，老猜想退休了，由於粗茶淡飯，半年一萬元就夠活了，預計領十年，老猜現在要存多少錢才夠？
同樣年息4%，4%/2=2%，一年複利兩次，十年二十次。計算如下：
P=＄10,000[1-(1+2%)^-20]/2%=＄163,54.33
　　以上複利公式數值可以自行計算，也有人已寫成Excel檔，可自行下載使用！ 下載
　　下次我們再來談年金的一些應用 　　　　　　　　　　　　　　　　　　　　　　　 結束

[猜謎人]

作者: cara551977

統計真的令人頭大

常常寫到後面自己也不知道在想什麼

就要從頭再思考一次了

不過商科的統計還算簡單

工科的統計~還真的要挑燈夜戰

我覺得應該是一樣

工科也不可能教常態分配的公式證明

也只是查表而已吧

[cara551977]

作者: 猜謎人

我覺得應該是一樣

工科也不可能教常態分配的公式證明

也只是查表而已吧

當然用查表阿

這玩意還要推導~學生會先衝去跳樓的

不過書本的難易度

以及老師教的深淺上

商科跟工科統計方面是有差異的

[猜謎人]

作者: cara551977

當然用查表阿

這玩意還要推導~學生會先衝去跳樓的

不過書本的難易度

以及老師教的深淺上

商科跟工科統計方面是有差異的

我覺得

都是一樣皮毛啦

從敘述統計到推論到無母數到變異數分析

反正也是要查表

只要沒公式的證明都是皮毛

[cara551977]

當初覺得教統計的老師好輕鬆唷

一堂課只需要教個幾題

大家就一個頭兩個大了

不像其他科~還要進度多少

一堂課看老師嘴都沒停過

一直講一直講很快一本書就講完了

[猜謎人]

作者: cara551977

當初覺得教統計的老師好輕鬆唷

一堂課只需要教個幾題

大家就一個頭兩個大了

不像其他科~還要進度多少

一堂課看老師嘴都沒停過

一直講一直講很快一本書就講完了

統計已經算是應用數學了
使用很簡單
但是如果推公式就難了

[cara551977]

作者: 猜謎人

統計已經算是應用數學了
使用很簡單
但是如果推公式就難了

猜葛葛~最近為何在專研統計阿??

[猜謎人]

作者: cara551977

猜葛葛~最近為何在專研統計阿??

以前學過啦

最近看卡通

[cara551977]

說真的現在的新聞實在看不下去

連續劇也好無聊

還是卡通好看

[猜謎人]

作者: cara551977

說真的現在的新聞實在看不下去

連續劇也好無聊

還是卡通好看

但是卡通也看不完

[cara551977]

作者: 猜謎人

但是卡通也看不完

這是真的

卡通真的好多唷

還好本人一向可以接受跳躍式看法

沒看到就算了

連看卡通都要堅持每集都看

那也太累了

[放下是真功夫]

複利的難.....

不是難在它的計算

是難在它的堅持　

人能夠堅持　投資的複利才有意義　

[放下是真功夫]

作者: cara551977

這是真的

卡通真的好多唷

還好本人一向可以接受跳躍式看法

沒看到就算了

連看卡通都要堅持每集都看

那也太累了

我也是跳躍式談話的人呦　

[猜謎人]

作者: cara551977

這是真的

卡通真的好多唷

還好本人一向可以接受跳躍式看法

沒看到就算了

連看卡通都要堅持每集都看

那也太累了

這樣看沒意思啦！

我都看他的用色、分鏡

因為以後畫圖有用

[K22514]

有些老師教數學 最後對學生說:
聽不懂的 自己去找參考書 ~~

[oya1340]

比我們老師好...報告不會寫唷..可以去参考護理協會論文看怎麼寫的...那我們就變無頭蒼蠅到處自己查了